Ultrasons laser et ondes elastiques guidées
Introduction
Les ondes élastiques guidées par réflexion, réfraction et conversion aux interfaces de structures telles que les cylindres, les plaques ou les tubes présentent des effets de dispersion remarquables. Pour les observer, les méthodes ultrasonores classiques nécessitent soit un contact mécanique avec le capteur piézoélectrique soit une immersion. Les techniques ultrasons laser combinant une source laser pour la génération thermoélastique et un interféromètre pour la détection présentent l’avantage d’être sans contact mécanique et très large bande. Elles sont donc particulièrement adaptées pour observer la propagation des ondes guidées sur de large gamme de fréquences et en particulier dans le cas d’interface complexes.
Les modes à vitesse de phase négative qui se propagent dans les guides d’ondes élastiques homogènes sont à la fois remarquables et courants. Ces modes ont la particularité d’avoir une vitesse de phase et une vitesse de groupe de sens opposés. De plus, au minimum de fréquence d’une branche à vitesse de phase négative, la vitesse de groupe s’annule tandis que la vitesse de phase reste finie : ceci donne lieu à une résonance locale. Nous exploitons les méthodes ultrasons laser pour explorer ces phénomènes et observer des effets de réflexion et réfraction négative ou de résonance.
1 - Réflexion et réfraction négative
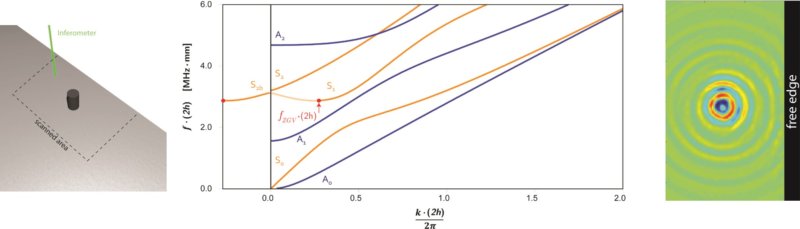
Depuis les travaux de Mindlin, plusieurs études sur les guides d’ondes élastiques ont confirmé l’existence d’ondes à vitesse de phase négative, pour lesquelles les fronts d’onde se propagent dans la direction opposée à celle de l’énergie. Ce phénomène se produit naturellement dans des milieux élastiques homogènes et en particulier dans les plaques. Nous avons exploité ces modes pour réaliser une lentille de Veselago dans une plaque élastique isotrope montrant une réfraction négative sur une bande de fréquences de largeur finie. Nous avons également étudié la réflexion négative en bord de plaque du mode S1 vers le mode S2b.
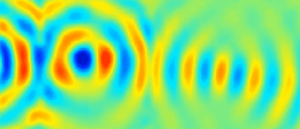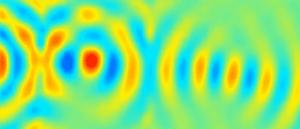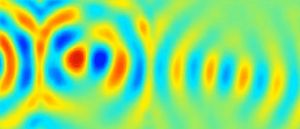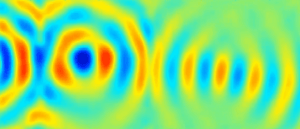
– S. Bramhavar, C. Prada, A. A. Maznev, A. G. Every, T. B. Norris, and T. W. Murray, "Negative refraction and focusing of elastic Lamb waves at an interface", Phys. Rev. B 83, 014106 (2011).
– F. D. Philippe, T. W. Murray, and C. Prada, "Focusing on Plates : Controlling Guided Waves using Negative Refraction", Scientific Reports 5, 11112 (2015)
– G. Gérardin. J. Laurent, C. Prada, and A. Aubry., "Negative reflection of Lamb waves at a free edge : Tunable focusing and mimicking phase conjugation.", J Acoust Soc Am. 140(1):591., (2016)
– D. Forcella, C. Prada, and R. Carminati, "Causality, Nonlocality, and Negative Refraction", Phys. Rev. Lett. 118, 134301, (2017)
– B. Gérardin, J. Laurent, F. Legrand, C. Prada, A. Aubry, "Negative reflection of elastic waves in complex environments, 2017
2 - Modes à vitesse de groupe nulle et applications à la caractérisation locale de plaques
La dispersion des ondes élastiques guidées dans les plaques, les cylindres ou les tubes est telle que pour certains modes, la vitesse de groupe peut s’annuler. En ces points particuliers des courbes de dispersion, désignés par ZGV pour Zero Group Velocity, le produit fréquence x épaisseur (d=2h) passe par un minimum alors que la vitesse de phase et la longueur de l’onde restent finies. Ils sont donc associés à des résonances locales.

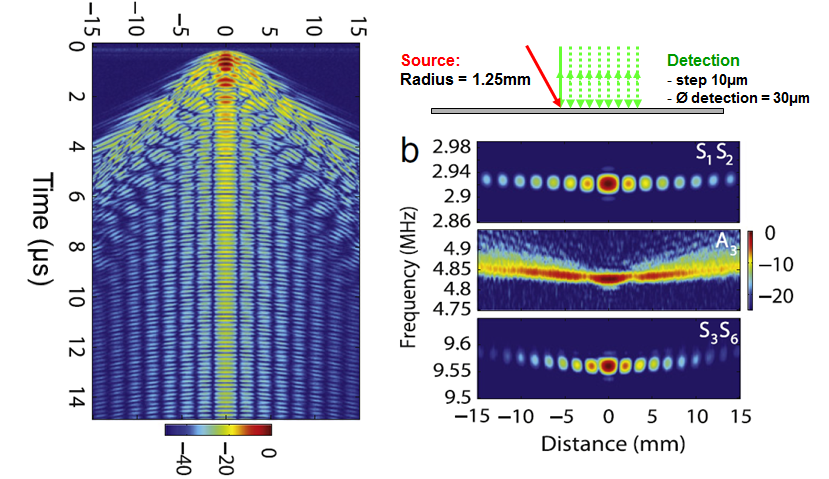
Dans nos expériences, ces modes à vitesse de groupe nulle sont engendrés par une impulsion laser brève. Le déplacement mécanique de la surface est détecté au même point à l’aide d’un interféromètre hétérodyne. Une fois éliminée la contribution due à l’échauffement local, le signal acoustique est dominé par les résonances associées aux modes à vitesse de groupe nulle. Les premières mesures en génération impulsionnelle ont été effectuées sur des plaques métalliques d’épaisseur millimétrique et nous avons montré qu’elles fournissaient une mesure très précise de l’épaisseur Clorennec et al. 2006. Nous avons étudié la décroissance temporelle de ces résonances particulières et comparé celles-ci aux résonances d’épaisseur Prada et al. 2008,Laurent et al. al. 2014.
Résonances ZGV et mesure sans contact du coefficient de Poisson
Le rapport des fréquences de résonance des deux premiers modes ZGV est indépendant de l’épaisseur de la plaque et dépend de manière biunivoque du coefficient de Poisson. Ainsi, il est possible de mesurer localement et précisément le coefficient de Poisson d’un solide isotrope, et les vitesses des ondes de volume si l’épaisseur est connue. Cette méthode sans contact a été testée sur une large gamme de matériaux, de plaques et de coques. Clorennec et al. 2007. Plus généralement, nous avons montré que le spectre des vibrations locales d’une plaque était entièrement gouverné par les résonances des modes ZGV. Ce phénomène est illustré sur la figure ci-dessous dans le cas de plaques de silice et de duralumin. Prada et al. 2008

Source thermoélastique et modes ZGV : contrôle et optimisation
Dans les métaux, la source laser est surfacique (dipôle de force) et se couple extrêmement bien avec les modes ZGV. Nous avons établi l’expression et vérifié expérimentalement le diamètre optimal d’un faisceau Gaussien pour générer un mode ZGV. De plus, un système lentille-Axicon a été adapté pour former une source annulaire de diamètre et largeur contrôlées afin d’augmenter l’amplitude des modes ZGV tout en restant sous le seuil d’ablation Bruno et al. 2016.


Nous avons étudié la génération des résonances ZGV dans des plaques de faible absorption optique. La source est alors volumique, l’amplitude des modes ZGV engendrés dépend de l’angle d’incidence du laser et de la longueur de pénétration optique Raetz et al. 2015.


Résonances ZGV dans les matériaux anisotropes
Dans les plaques anisotropes, les courbes de dispersion dépendent de la direction de propagation et il existe également des modes ZGV. Les mesures que nous avons effectuées avec une source laser ponctuelle sur une galette de silicium révèlent deux résonances ZGV au voisinage de la résonance d’épaisseur. En utilisant une ligne source qui favorise une direction de propagation, on observe alors une seule résonance ZGV dont la fréquence et l’amplitude varient avec la direction de la source Clorennec et al. 2009. Ceci permet, par exemple, la mesure sans contact de l’anisotropie de plaques métalliques obtenues par laminage.

Nous avons utilisé la même approche pour mesurer l’anisotropie dans des tubes de Zircaloy. Le contrôle de l’intégrité de ces tubes, utilisés pour confiner le combustible dans les réacteurs à eau pressurisée, présente un intérêt majeur pour l’industrie nucléaire. Pour améliorer les méthodes de contrôle ultrasonore, il est important de connaitre les constantes élastiques. En mesurant le spectre des résonances ZGV pour les ondes axiales et circonférentielles, nous avons pu estimer les 5 constantes élastiques sous l’hypothèse d’un milieu transverse isotrope Cès et al. 2012.

Enfin, nous avons mis en évidences les nombreux modes à vitesse de groupe nulle dans les cylindres. Nous avons mesuré le spectre des résonances associées à ces modes ZGV dans des tiges de section sub-millimétriques et avons montré qu’elles pouvaient être utilisées pour déterminer les constantes élastiques Laurent et al. 2015.


Résonances ZGV dans les plaques collées
Les modes Lamb à vitesse de groupe nulle (ZGV) peuvent être utilisés pour évaluer le couplage entre deux plaques solides liées par une couche mince. Si l’épaisseur du est négligeable, le couplant peut être modélisé par des raideurs interfaciales normales et tangentielles. Nous avons montré pour une structure bicouche symétrique, que les fréquences de résonances ZGV étaient fonction de ces raideurs interfaciales.

Les modes ZGV ont été étudiées dans une structure composée de deux plaques collées par une couche adhésive. Les courbes de dispersion ont été calculées pour un échantillon Duralumin/époxy/Duralumin, où l’adhérence a été modélisée par un ressort normal et tangentiel aux deux interfaces. Plusieurs modes ZGV ont été identifiés et leur dépendance en fonction des raideurs interfaciales et de l’épaisseur de la couche adhésive ont été étudiées numériquement. Des expériences ont été réalisées par méthode LU. Les résonances locales (ZGV) ont été mesurées en utilisant une source et sonde laser superposées. Connaissant les épaisseurs et les constantes élastiques des couches de Duralumin et d’époxy, la comparaison entre les résonances ZGV théoriques et expérimentales à conduit à une évaluation des raideurs interfaciales. Un bon accord avec les courbes de dispersion théoriques confirme l’identification des résonances et des estimations des paramètres. Cette technique sans contact est prometteuse pour l’évaluation locale des structures collées.

Détection et caractérisation de films minces
Nous avons étudié l’influence du dépôt d’un film mince ( 100nm) sur les résonances ZGV d’une plaque millimétrique. Il apparait que le résonateur constitué par le substrat et le film était sensiblement différent d’un résonateur à Quartz. En effet, pour un résonateur à Quartz, une couche mince déposée engendre une variation relative de fréquence de résonance égale et opposée à la variation relative de masse. Nous avons montré que dans le cas des résonances ZGV, la relation suivante était satisfaite
Le facteur de proportionnalité K dépend à la fois du substrat et de la couche déposée. Les valeurs de K peuvent être très différentes de 1, par exemple, K=1.16 pour de l’or déposée sur du Duralumin, K=0.3 pour du carbure de silicium déposé sur du Duralumin, et même K=-0.48 pour du carbure de silicium déposé sur du cuivre. Théoriquement, on peut donc en déposant une couche mince augmenter la fréquence de résonance. Ceci reste toutefois à vérifier expérimentalement.
Nous avons montré que l’on pouvait estimer l’épaisseur de films d’or de 100 à 500nm déposés sur une plaque de Duralumin de 1.5mm d’épaisseur, depuis la face opposée. Cès et al. 2011.

De la résonance ZGV à la résonance de bord
Les modes à vitesse de groupe nulle sont des solutions particulières de l’équation de Rayleigh-Lamb pour une plaque infinie. En pratique, il est important d’étudier les phénomènes mis en jeu près des bords afin de comprendre les facteurs qui limitent les applications des méthodes ZGV. Nous avons observé expérimentalement, sur différents matériaux, une transition abrupte entre la résonance ZGV du mode S1S2 et la résonance de bord qui apparaît à une fréquence sensiblement inférieure. La figure ci-dessous montre le spectre des résonances locales mesuré sur une plaque de Duralumin pour différentes distances entre la source et le bord de la plaque. On observe que cette transition a lieu à une distance du bord voisine de l’épaisseur de la plaque Cès et al. 2011.

A droite : fréquences de résonances normalisées en fonction du coefficient de Poisson du matériau.
Publications sur les modes à vitesse de groupe nulle :
– Prada C, Balogun O, Murray TW, Laser-based ultrasonic generation and detection of zero-group velocity Lamb waves in thin plates, Appl. Phys. Lett. 87 (19) : 2005.
– Clorennec D, Prada C, Royer D, Laser impulse generation and interferometer detection of zero group velocity Lamb mode resonance, Appl. Phys. Lett. 89 (2) : 2006.
– Clorennec D, Prada C, Royer D, Local and noncontact measurements of bulk acoustic wave velocities in thin isotropic plates and shells using zero group velocity Lamb modes, J. Appl. Phys. 101 (3) : 2007.
– Prada C, Clorennec D, Royer D, Power law decay of zero group velocity Lamb modes, Wave Motion 45 (6), 2008.
– Prada C, Clorennec D, Royer D, Local vibration of an elastic plate and zero-group velocity Lamb modes, J. Acoust. Soc. Am. 124 (1), 2008.
– Royer D, Clorennec D, Prada C, Caractérisation de plaques et de tubes par modes de Lamb à vitesse de groupe nulle, Instrumentation Mesure Métrologie, Vol 10/1-2, pp.73-94, 2010
– M. Cès, D. Clorennec, D. Royer, C. Prada, Edge resonance and Zero Group Velocity Lamb modes in a free elastic plate, J. Acoust. Soc. Am. 130, 2, pp. 689-694 (2011). JASA_2011
– M. Cès, D. Clorennec, D. Royer, C. Prada, Thin layer thickness measurements by Zero Group Velocity Lamb mode resonances, Rev. Sci. Instr. 82, 114902 (2011).
– M. Cès, D. Royer, C. Prada, Characterization of mechanical properties of a hollow cylinder with zero group velocity Lamb modes, J. Acoust. Soc. Am. 132 (1), (2012)
– J. Laurent, D. Royer, C. Prada, Temporal behavior of local plate resonances, Wave Motion 51 (6), pp 1011–1020, (2014)
– S. Mezil, J. Laurent, D. Royer, C. Prada, "Non-contact probing of interfacial stiffnesses between two plates by zero-group velocity Lamb modes", Appl. Phys. Lett. 105, 021605 (2014).
– S. Mezil, F. Bruno, S. Raetz, J. Laurent, D. Royer and C. Prada, "Investigation of interfacial stiffnesses of a tri-layer using Zero-Group Velocity Lamb modes" J. Acoust. Soc. Am. 138 (5), 3202-3209 (2015).
– J. Laurent, D. Royer, T. Hussain, F. Ahmad, C. Prada, Laser induced Zero-Group Velocity resonances in Transversely Isotropic cylinder, J. Acoust. Soc. Am. 137 (6), (2015).
– F. Bruno, J. Laurent, P. Jehanno, D. Royer, C. Prada, "Laser beam shaping for enhanced Zero-Group Velocity Lamb modes generation", J. Acoust. Soc. Am. 140 (4), 2829-2838 (2016).
– S Raetz, J Laurent, T Dehoux, D Royer, B Audoin, C Prada, "Effect of light refraction on the photoelastic generation of ZGV Lamb modes in optically low-absorbing plates", J. Acoust. Soc. Am. 138 (6), 3522-3530 (2016)










